Question

Find the slope of the altitude on each side of triangle ABC. (b) A(4,0), B(0,4), C(0,0)

Answer 1

We are given a triangle with the following vertices

A(4, 0)

B(0, 4)

C(0, 0)

Let us draw the altitude on each side of triangle ABC

As you can see, we have drawn the altitude on each side of the triangle.

The slopes of these altitudes are given by

`\begin{gathered} slope\: AD=-(1)/(slope\: BC) \\ slope\: BE=-(1)/(slope\: AC) \\ slope\: CF=-(1)/(slope\: AB) \end{gathered}`

Slope BC:

B(0, 4) and C(0, 0)

Slope AC:

A(4, 0) and C(0, 0)

`slope\: AC=(y_2−y_1)/(x_2−x_1)=(0-0)/(0-4)=(0)/(-4)=0\: \quad (\text{horizontal line)}`

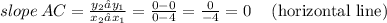
Slope AB:

A(4, 0) and B(0, 4)

`slope\: AB=(y_2−y_1)/(x_2−x_1)=(4-0)/(0-4)=(4)/(-4)=-1`

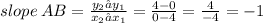
As you can see, only the slope of altitude CF exists.

`slope\: CF=-(1)/(slope\: AB)=-(1)/(-1)=1`

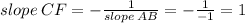
Therefore, the slope of altitude CF is found to be 1