For the linear regression the dependent and independent variables are:
y: "weight of a woman" (measured in pounds)
x: "height of a woman" (measured in inches)
You have to calculate the estimated linear regression equation:
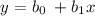
Where
b₀ is the estimate of the y-intercept
b₁ is the estimate of the slope
To calculate both by hand you have to use the following formulas:
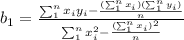
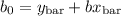
y bar and x bar are the sample means for the weight and height
n is the number of women observed, in this case the sample size is
n=5 women
Next calculate the needed summatories, i.e. add each obervation from the corresponding variables
∑xi= 335
∑xi²= 22455
∑yi=670
∑xiyi=44962
ybar=∑yi/n= 670/5=134 pounds
xbar=∑xi/n= 335/5=67 inches
Replace the values in the formulas:
Slope:
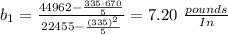
y-intercept
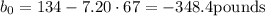
The estimated linear equation is:
y=-348.4+7.20x
b)
The y-intercept of the linear regression indicates the value of the estimated mean of the variable y when x equals zero.
The slope of the linear regresion insicates the change of the estimated mean of the variable y when the variable x increases one unit.
So in terms of this exercise you can interpret the y-intercept as:
-348.4pounds is the estimated average weight of women when their height is zero inches.
→ Note that this interpretation has no logical meaning, at least not one applicable in real life, but for the regression is a valid mathematical result and interpretation.
And the slope can be interpreted as:
7.2pounds/inches is the modification of the estimated average weight of weomen when their height increases 1 inch.