Question

I really need it to be sold in imaginary numbers

Answer 1

Solving a 5th grade polynomial

We want to find the answer of the following polynomial:

`x^5+3x^4+3x^3+19x^2-54x-72=0`

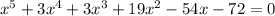
We can see that the last term is -72

We want to find all the possible numbers that can divide it. Those are:

{±1, ±2, ±3, ±4, ±6, ±8, ±9, ±12, ±18, ±36, ±72}

We want to factor this polynomial in order to find all the possible x-values. In order to factor it we will have to find some binomials that can divide it using the set of divisors of -72.

We know that if

(x - z) is a divisor of this polynomial then z might be a divisor of the last term -72.

We will verify which is a divisor using synthetic division. If it is a divisor then we can factor using it:

Let's begin with

(x-z) = (x - 1)

We want to divide

`((x^5+3x^4+3x^3+19x^2-54x-72))/(x-1)`

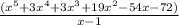
Using synthetic division we have that if the remainder is 0 it will be a factor

We can find the remainder by replacing x = z in the polynomial, when it is divided by (x - z). It is to say, that if we want to know if (x -1) is a factor of the polynomial we just need to replace x by 1, and see the result:

If the result is 0 it is a factor

If it is different to 0 it is not a factor

Replacing x = 1

If we replace x = 1, we will have that:

`\begin{gathered} x^5+3x^4+3x^3+19x^2-54x-72 \\ \downarrow \\ 1^5+3\cdot1^4+3\cdot1^3+19\cdot1^2-54\cdot1-72 \\ =1+3+3+19-54-72 \\ =-100 \end{gathered}`

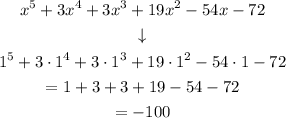
Then the remainder is not 0, then (x - 1) is not a factor.

Similarly we are going to apply this until we find factors:

(x - z) = (x + 1)

We replace x by -1:

`\begin{gathered} x^5+3x^4+3x^3+19x^2-54x-72 \\ \downarrow \\ (-1)^5+3\cdot(-1)^4+3\cdot(-1)^3+19\cdot(-1)^2-54\cdot(-1)-72 \\ =-1+3-3+19+54-72 \\ =0 \end{gathered}`

Then, (x + 1) is a factor.

Using synthetic division we have that:

Then:

`x^5+3x^4+3x^3+19x^2-54x-72=(x+1)(x^4+2x^3+x^2+18x-72)`

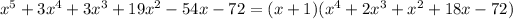
Now, we want to factor the 4th grade polynomial.

Let's remember our possibilities:

{±1, ±2, ±3, ±4, ±6, ±8, ±9, ±12, ±18, ±36, ±72}

Since we verified ±1, let's try with ±2 as we did before.

(x - z) = (x - 2)

We want to divide:

`(x^4+2x^3+x^2+18x-72)/(x-2)`

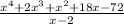
We replace x by z = 2:

`\begin{gathered} x^4+2x^3+x^2+18x-72 \\ \downarrow \\ 2^4+2\cdot2^3+2^2+18\cdot2-72 \\ =16+16+4+36-72 \\ =0 \end{gathered}`

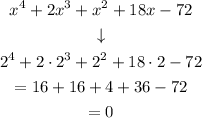
Then (x - 2) is a factor. Let's do the synthetic division:

Then,

`x^4+2x^3+x^2+18x-72=(x-2)(x^3+4x^2+9x+36)`

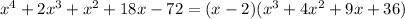
Then, our original polynomial is:

`\begin{gathered} x^5+3x^4+3x^3+19x^2-54x-72 \\ =\mleft(x+1\mright)\mleft(x^4+2x^3+x^2+18x-72\mright) \\ =(x-1)(x-2)(x^3+4x^2+9x+36) \end{gathered}`

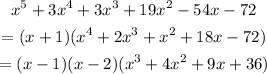
Now, let's prove if (x +2) is a factor, using the new 3th grade polynomial.

(x - z) = (x + 2)

We replace x by z = -2:

`\begin{gathered} x^3+4x^2+9x+36 \\ \downarrow \\ (-2)^3+4(-2)^2+9(-2)+36 \\ =-8+16-18+36 \\ =26 \end{gathered}`

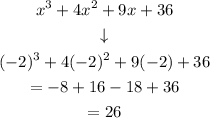
Since the remainder is not 0, (x +2) is not a factor.

All the possible cases are:

{±1, ±2, ±3, ±4, ±6, ±8, ±9, ±12, ±18, ±36, ±72}

let's prove with +4

(x - z) = (x + 4)

We want to divide:

`(x^3+4x^2+9x+36)/(x+4)`

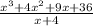
Let's replace x by z = -4 in order to find the remainder:

`\begin{gathered} x^3+4x^2+9x+36 \\ \downarrow \\ (-4)^3+4(-4)^2+9(-4)+36 \\ =-64+64-36+36 \\ =0 \end{gathered}`

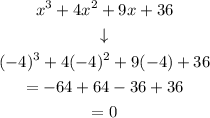
Then (x + 4) is a factor. Let's do the synthetic division:

Then,

`x^3+4x^2+9x+36=(x+4)(x^2+9)`

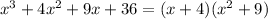
Since

x² + 9 cannot be factor, we have completed our factoring:

`\begin{gathered} x^5+3x^4+3x^3+19x^2-54x-72 \\ =(x-1)(x-2)(x^3+4x^2+9x+36) \\ =(x-1)(x-2)(x+4)(x^2+9) \end{gathered}`

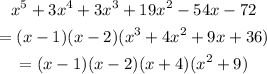
Now, we have the following expression:

`(x-1)(x-2)(x+4)(x^2+9)=0`

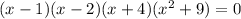
Then, we have five posibilities:

(x - 1) = 0

or (x - 2) = 0

or (x + 4) = 0

or (x² + 9) = 0

Then, we have five solutions;

x - 1 = 0 → x₁ = 1

x - 2 = 0 → x₂ = 2

x + 4 = 0 → x₃ = -4

x² + 9 = 0 → x² = -9 → x = ±√-9 = ±√9√-1 = ±3i

→ x₄ = 3i

→ x₅ = -3i

Answer- the solutions of the polynomial are: x₁ = 1, x₂ = 2, x₃ = -4, x₄ = 3i and x₅ = -3i