x intercept is -5
Step-by-step explanation
Step 1
find the slope of the line:
when you know 2 points of the line, you can find the slope, by using:
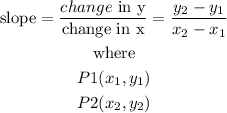
then,Let
P1(33,-22)
P2(52,-33)
replace,
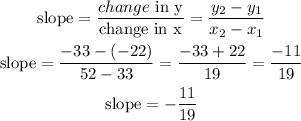
Step 2
find the equation of the line
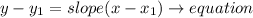
let
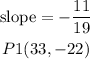
replace,
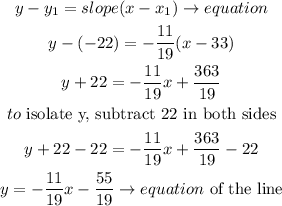
now, we have the equation of the line, to get the x intercetp ( it is when y=0)
replace

so, the x intercetp is -5.
I hope this helps you