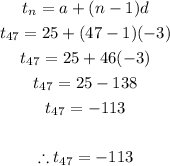Question

Given t3 = 19 and t15 = −17 in an arithmetic sequence, find t47

Answer 1

Let's begin by identifying key information given to us:

This is an Arithmetic Sequence

`\begin{gathered} t_3=19 \\ t_(15)=-17 \\ t_(47)=? \end{gathered}`

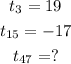
An Arithmetic Sequence is defined by the formula:

`\begin{gathered} t_n=a+(n-1)d \\ \Rightarrow t_3=a+(3-1)d \\ \Rightarrow a+2d=19 \\ a+2d=19------1 \\ \\ \Rightarrow t_(15)=a+(15-1)d \\ \Rightarrow a+14d=-17----2 \\ a+14d=-17----2 \end{gathered}`

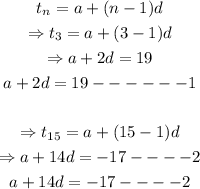
We will proceed to solve both equations simultaneously as shown below:

`\begin{gathered} a+2d=19------1 \\ a+14d=-17----2 \\ \text{Subtract equation 1 from 2, we have:} \\ a-a+14d-2d=-17-19 \\ 12d=-36 \\ d=-(36)/(12)=-3 \\ d=-3 \\ \text{Substitute ''d'' into equation 1, we have:} \\ a+2(-3)=19 \\ a-6=19 \\ a=19+6 \\ a=25 \end{gathered}`

Since we know the values of ''a'' & ''d'', we will proceed to solve for t47

`\begin{gathered} t_n=a+(n-1)d \\ t_(47)=25+(47-1)(-3) \\ t_(47)=25+46(-3) \\ t_(47)=25-138 \\ t_(47)=-113 \\ \\ \therefore t_(47)=-113 \end{gathered}`