Question

Hi, can you help me answer this question please, thank you!

Answer 1

To solve this problem, we just need to use the margin of error formula. This formula is given by

`ME=z*\frac{\sigma}{\sqrt[]{n}}`

Where ME is our margin of error, sigma is the standard deviation, n is the sample size, and z is the critical value(associated with the confidence level).

From the text, we have:

`\begin{gathered} n=23 \\ \sigma=13.7 \\ z(0.80)=1.32 \end{gathered}`

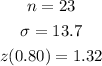
Plugging those values in our equation, we have

`ME=1.32*\frac{13.7}{\sqrt[]{23}}=\frac{18.084}{\sqrt[]{23}}=3.77077466381\ldots\approx3.8`

And this is our margin of error.