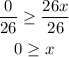Question

Barbara 13) 26+ m 2 5(-6 + 3m) 2 сын 216>14/21 14) 20 - 2p>-23(x-4) - (-4) 20-apa-ap-4+up 20-20-up>-4-ro 26-2p>P p>-24 20:2p>z-ap- 学部 16) -6(1 + 6x) < 6(1 - 5x) -19 Tz72ix eis xs-2 Pad2e -EclHEX 1-3 x 6x-bed-1 껏 t6>- TSX> 1- 4r) < -2(r + 3) - 4 18) -6(1 + 2x) > 6(2x - 1) + 2x L2R - 4 L SR-22 KGA

Answer 1

Answer: x less equal to 0

`0\ge*`

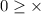
Step by step solution:

To solve the inequality:

`-6(1+2x)\ge6(2x-1)+2x`

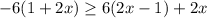
We start by taking out the parenthesis:

`-6-12x\ge12x-6+2x`

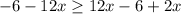
We are going to add +12 on both sides:

`\begin{gathered} -6-12x+12x\ge12x-6+2x+12x \\ -6\ge26x-6 \end{gathered}`

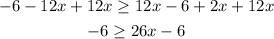
Adding +6 to each of the sides, left and right, to maintain the balance of the inequality, each operation must be performed on both sides:

`\begin{gathered} -6+6\ge26x-6+6 \\ 0\ge26x \end{gathered}`

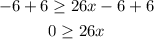
Now we divide each side by 1/26:

`\begin{gathered} (0)/(26)\ge(26x)/(26) \\ 0\ge x \end{gathered}`