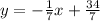Question

Line m passes through points (-6, -5) and (-4, 1) as shown on the coordinate grid.  Line l is perpendicular to line m and contains the point (6, 4). Determine the equation of line l.

Answer 1

First we need to find the slope of line m.

The slope of a line is:

`\begin{gathered} P_1=(x_1,y_1),P_2=(x_2,y_2)_{} \\ m=((y_2-y_1))/((x_2-x_1)) \end{gathered}`

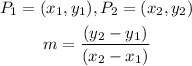
For line m we know P1=(-6,-5) and P2=(-4, 1), so the slope of m is:

`\begin{gathered} m=((1-(-6)))/((-4-(-5))) \\ m=(1+6)/(-4+5)=(7)/(1)=7 \end{gathered}`

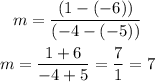
Now, if two lines are perpendicular the slopes satisfy the following equation:

`m_2=-(1)/(m_1)`

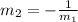
The slope of line l is:

`\begin{gathered} We\text{ call m2 the slope of line l and m1 the slope of line m:} \\ m_2=-(1)/(m_1)=-(1)/(7) \end{gathered}`

Finally, the line l pass througth point (6, 4), so the equation is:

`\begin{gathered} y=m_2x+b \\ 4=-(1)/(7)\cdot6+b_{} \\ b=4+(6)/(7)=(4\cdot7+6)/(7) \\ b=(28+6)/(7) \\ b=(34)/(7) \end{gathered}`

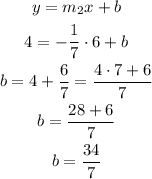
So, teh equation of line l is:

`y=-(1)/(7)x+(34)/(7)`