Question

Study the diagram a tree casts a shadow that is 150ft long, The angle of elevation from the tip of the shadow to the top of the tree is 30°

Answer 1

First, consider the following right triangle:

For angle A, the tangent of the angle is defined as follows:

`\tan (A)=(x)/(h)`

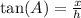
In our case, recall that we have the following triangle

So using the previous definition, we have the following

`\tan (30)=\frac{tree\text{ height}}{150}`

so, if we multiply both sides of the equation by 150 we get

`tree\text{ height = tan(30)}\cdot150`

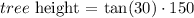
using a calculator, we get that the height of the tree is approximately 86.6 feet (87 feet)