First, let's calculate the horizontal and vertical components of the wind speed (W) and the airplane speed (A), knowing that south is a bearing of 270° and northeast is a bearing of 45°:
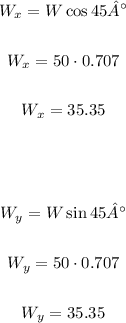
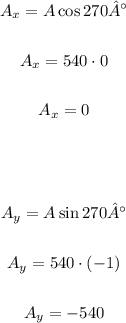
Now, let's add the components of the same direction:
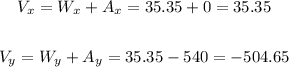
To find the resultant bearing (theta), we can use the formula below:
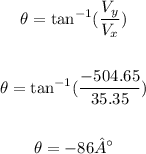
The angle -86° is equivalent to -86 + 360 = 274°.
Therefore the correct option is b.