Question

1. Match the graphs of the derivatives to the graphs of their functions. Use what you know about the meaning of the derivative, and use key points on both graphs to be sure your answers make sense.

Answer 1

A) The given function is,

`f(x)=e^x`

Its derivative will be,

`f^(\prime)(x)=e^x`

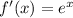
The graph of the derivative can be drawn as,

Thus, option (G) is correct for (A).

(B).

The given function is,

`\begin{gathered} f(x)=\ln \lvert x\rvert \\ f^(\prime)(x)=(1)/(x) \end{gathered}`

The graph of the derivative (1/x) can be drawn as,

Thus, option (F) is correct for (B).

(C) The given function is,

`\begin{gathered} f(x)=ln\lvert\sec x\rvert \\ f^(\prime)(x)=(\sec x\tan x)/(\sec x)=\tan x \end{gathered}`

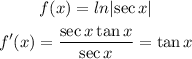
The graph of the derivative i.e the tanx can be drawn as,

Thus, the option (E) is correct for (C).

(D) The given function is,

`\begin{gathered} f(x)=\ln \lvert\sec x+\tan x\rvert \\ f^(\prime)(x)=(1)/(\sec x+\tan x)*(\sec x\tan x+\sec ^2x) \\ f^(\prime)(x)=\sec x \end{gathered}`

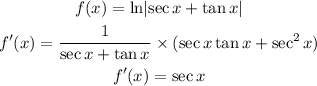
The derivative of the function is secx whose graph can be drawn as,

Thus, option (H) is the correct option for (D).