ANSWER
852 ft²
Step-by-step explanation
The gable is a triangle with two sides of 42 feet - which means that it is an isosceles triangle, that meet at a 105° angle. To find the area, we need to find the length of the base, b, and the height, h, of this triangle.
The height is also the height of the two right triangles formed by the blue line in the diagram above. Both triangles are congruent, so the base of each of these is half the base of the gable. The blue line showing the height divides the 105° angle in two - i.e. it is the angle bisector. Thus, we have two congruent triangles with measures,
Using trigonometric ratios, we can find the values of h and a.
The height, h, is the adjacent side to the 52.5° angle and we know the length of the hypotenuse, 42 ft. To find h, we have to use the cosine of the angle,
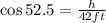
Solving for h,

The base, a, is the opposite side to the 52.5° angle, so, to find it, we have to use the sine of the angle,
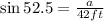
Solving for a,
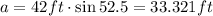
The area of one of the right triangles is,
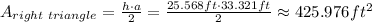
The gable is formed by two of these right triangles, so the area of the gable is twice the area of this right triangle,
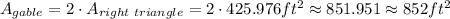
Hence, the area of the gable is 852 square feet, rounded to the nearest square foot.