Question

Write a system of equations to describe the situation below, solve using elimination, and fill in the blanks.The manager at a community pool is looking over receipts. On a certain Monday, the pool had 23 children and 39 adults, which brought in $202. That same week on Tuesday, 25 children and 44 adults came to the pool, which brought in $226. What are the admission prices for children and adults?

Answer 1

Let c represent the admission price for 1 child

Let a represent the admission price for 1 adult

On Monday, the pool had 23 children and 39 adults, which brought in $202

This can be represented as

23c + 39a = 202________________equation(1)

On Tuesday, 25 children and 44 adults came to the pool, which brought in $226

This can be represented as

25c + 44a = 226________________equation(2)

We are asked to solve the equations using elimination Method.

23c + 39a = 202________________equation(1)

25c + 44a = 226________________equation(2)

Let us eliminate c

Multiply equation (1) by 25 and equation (2) by 23

We have

575c + 975a = 5050_________equation (3)

575c + 1012a = 5198__________equation (4)

Subtract equation (4) from equation (3)

-37a = -148

Divide both sides by -37

`\begin{gathered} (-37a)/(-37)=(-148)/(-37) \\ a=4 \end{gathered}`

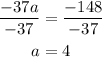
Substitute a = 4 into equation (1)

23c + 39a = 202

23c + 39(4) = 202

23c + 156 = 202

23c = 202 - 156

23c = 46

Divided both sides by 23

`\begin{gathered} (23c)/(23)=(46)/(23) \\ c=2 \end{gathered}`

Hence, a = 4, c = 2

The admission price for children is $2 while that of adults is $4