Question

Given cot A =9/2 and that angle A is in Quadrant I, find the exact value of sin A in simplest radical form using a rational denominator.

Answer 1

Since we have that cot(A)=9/2, then its inverse function tangent is:

`\tan (A)=(2)/(9)`

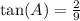
We have that angle A is on quadrant I, and we also know the following about the tangent function:

`\tan (A)=\frac{\text{opposite side}}{adjacent\text{ side}}`

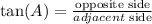
then, we can draw angle A with this information:

Notice that we get the following right triangle:

Then, we can find the hypotenuse using the pythagorean theorem:

`\begin{gathered} c=\sqrt[]{9^2+2^2}=\sqrt[]{81+4}=\sqrt[]{85} \\ \Rightarrow c=\sqrt[]{85} \end{gathered}`

now that we have all the measures of the triangle, we can calculate sin(A):

`\begin{gathered} \sin (A)=\frac{\text{opposite side}}{hypotenuse}=\frac{2}{\sqrt[]{85}} \\ \Rightarrow\sin (A)=\frac{2}{\sqrt[]{85}} \end{gathered}`

therefore, sin(A) = 2/sqrt(85)