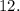Question

Find the common ratio and the number of terms in the given finite geometric sequence.a_n={2,1, \frac{1}{2} ,..., \frac{1}{1024} }The common ratio is AnswerThere are Answer terms.

Answer 1

Notice that:

`\begin{gathered} 1=2*(1)/(2), \\ (1)/(2)=1*(1)/(2). \end{gathered}`

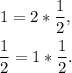
Therefore, the common ratio is:

`(1)/(2).`

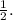
The mth term of the sequence has the general form:

`a_m=2((1)/(2))^(m-1).^`

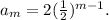
Setting

`a_m=(1)/(1024),`

we get:

`(1)/(1024)=2((1)/(2))^(m-1).`

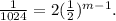
Solving the above equation for m, we get:

`\begin{gathered} (1)/(2*1024)=(1)/(2^(m-1)), \\ 2048=2^(m-1), \\ log_2(2048)=m-1(log_22), \\ 11=m-1, \\ m=11+1, \\ m=12. \end{gathered}`

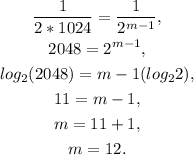
Finally, we get that there are

`12`

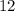
terms in the finite geometric sequence.

Answer:

First blank:

`(1)/(2),`

Second blank:

`12.`