Question

Joey has $0.75 in Dimes and Nickels.He has a total of 10 coins..How many Dimes and nickels are there?

Answer 1

Given:

Total amount = $0.75

Total number of coins = 10

Let's find the number of Dimes and nickels.

Apply the standard unit, where:

1 dime = $0.10

1 nickel = $0.05

Let d represent number of dimes and let n represent number of nickels.

We have the set of equations:

d + n = 10......................equation 1

0.10d + 0.05n = 0.75.........equation 2

Let's solve both equations simultaneously using substitution method.

Rewrite equation 1 for d:

d = 10 - n..................equation 3

Substitute (10 - n) for d in equation 2:

0.10(10 - n) + 0.05c = 0.75

Apply distributive property:

0.10(10) + 0.10(-n) + 0.05c = 0.75

1 - 0.10n + 0.05n = 0.75

1 - 0.05n = 0.75

Subtract 1 from both sides:

1 - 1 - 0.05n = 0.75 - 1

-0.05n = -0.25

Divide both sides by -0.05:

`\begin{gathered} (-0.05n)/(-0.05)=(-0.25)/(-0.05) \\ \\ n=5 \end{gathered}`

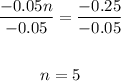
Substitute 5 for n in equation 3:

d = 10 - n

d = 10 - 5

d = 5

Therefore, we have:

n = 5, d = 5

Therefore, there are 5 Dimes and 5 nickels.

ANSWER:

5 Dimes and 5 nickels.