Question

How many ways can Marie choose two pizza toppings from a menu with eight toppings if each topping can only be chosen once

Answer 1

Given:

There are given that the 8 toppings on the menu.

Step-by-step explanation:

According to the question:

We need to find a number of ways that choose 2 pizzas with toppings from the menu of 8 toppings.

Then,

To find the number of ways, we need to use the combination formula:

So,

From the combination of the formula:

`nC_r=(n!)/(r!(n-r)!)`

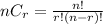
Where,

`\begin{gathered} n=8 \\ r=2 \end{gathered}`

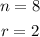
Then,

Put both values into the given formula:

`\begin{gathered} nC_(r)=(n!)/(r!(n-r)!) \\ 8C_2=(8!)/(2!(8-2)!) \end{gathered}`

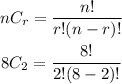
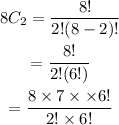
Then,

`\begin{gathered} 8C_(2)=(8!)/(2!(8-2)!) \\ =(8!)/(2!(6!)) \\ =(8*7**6!)/(2!*6!) \end{gathered}`

Then,

Final answer:

Hence, the number of ways is 28.