A general equation for a line in the slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
Given the equation:
y = 3 - 2x
Which, in the slope-intercept form is:
y = -2x + 3
That is, the slope is -2.
To find the parallel line, let's write the options in the slope-intercept form too. Parallel lines have the same slope.
1) 4x + 2y = 5
To put it in the slope-intercept form, let's subtract 4x from both sides and then divide the sides by 2:
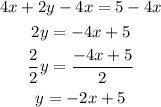
Slope = -2. The lines have the same slope (-2) and thus are parallels.
2) 2x + 4y = 1
To put it in the slope-intercept form, let's subtract 2x from both sides and then divide the sides by 4:
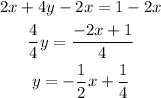
Slope = -1/2.
The equations have different slopes. So, they are not parallel.
3) y = 3 - 4x
To write it in the slope-intercept form, just organize the order of the terms on the second side of the equation.
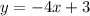
Slope = -4.
The equations have different slopes. So, they are not parallel.
4) y = 4x - 2
The equation is in the slope-intercept form.
Slope 4. The equations have different slopes. So, they are not parallel.
Answer: 4x+ 2y = 5 is parallel to y = 3 - 2x.