Question

A54С3BFind sin(ZABC + 60°).

Answer 1

The given expression is

`\sin (\angle ABC+\mathring{60})`

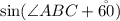
At first, we will use this rule to solve the question

`\sin (A+B)=\sin A\cos B+\cos A\sin B`

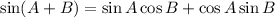
By using this rule with the given expression, then

`\sin (\angle ABC+\mathring{60})=\sin \angle ABC\cos 60+\cos \angle ABC\sin 60`

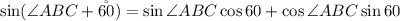
From the given triangle

`\begin{gathered} \sin \angle ABC=(AC)/(AB) \\ \sin \angle ABC=(4)/(5) \\ \cos \angle ABC=(BC)/(AB) \\ \cos \angle ABC=(3)/(5) \end{gathered}`

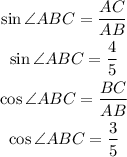
Since angle 60 is a special angle then

`\begin{gathered} \sin 60=\frac{\sqrt[]{3}}{2} \\ \cos 60=(1)/(2) \end{gathered}`

Let us substitute these values in the rule above

`\sin (\angle ABC+60)=((4)/(5))((1)/(2))+((3)/(5))(\frac{\sqrt[]{3}}{2})_{}`

Simplify the right side

`\sin (\angle ABC+60)=(2)/(5)+(3)/(10)\sqrt[]{3}`

The correct answer is B