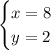Question

Solve using substitution. -2x +y = -14 and 3x - 8y =8

Answer 1

To solve the system of equations using the substitution method, first solve for a variable from one of the equations.

For example, you can solve for y from the first equation, like this

`\begin{cases}-2x+y=-14\text{ Equation 1} \\ 3x-8y=8\text{ Equation 2}\end{cases}`
`\begin{gathered} -2x+y=-14 \\ \text{ Add 2x from both sides of the equation} \\ -2x+y+2x=-14+2x \\ y=-14+2x \end{gathered}`

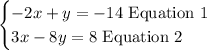
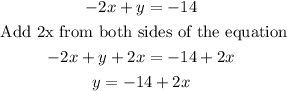
Now, replace the value of y into the second equation:

`\begin{gathered} 3x-8y=8 \\ 3x-8(-14+2x)=8 \end{gathered}`

And solve for x

`\begin{gathered} 3x-8(-14+2x)=8 \\ \text{ Apply distributive property} \\ 3x+112-16x=8 \\ \text{ Subtract 112 from both sides of the equation} \\ 3x+112-16x-112=8-112 \\ 3x-16x=8-112 \\ \text{ Operate similar terms} \\ -13x=-104 \\ \text{ Divide by -13 into both sides of the equation} \\ (-13x)/(-13)=(-104)/(-13) \\ x=8 \end{gathered}`

Finally, replace the value of x in any of the initial equations, for example, the first

`\begin{gathered} -2x+y=-14 \\ -2(8)+y=-14 \\ -16+y=-14 \\ \text{ Add 16 from both sides of the equation} \\ -16+y+16=-14+16 \\ y=2 \end{gathered}`

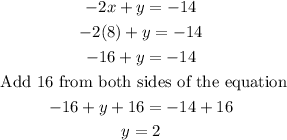
Therefore, the solutions of the system of linear equations are

`\begin{cases}x=8 \\ y=2\end{cases}`