We are given the following equation of a circle.
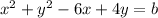
Recall that the standard form of the equation of a circle is given by
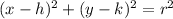
Where (h, k) are the coordinates of the center and r is the radius of the circle.
Let us convert the given equation into the standard form to find out the coordinates of the center.
We can use completing the square method for the conversion.
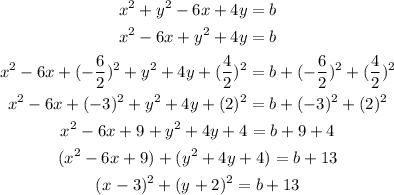
So, the coordinates of the center are
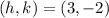
Therefore, the y-coordinate of the center is -2
Since the radius of the circle is 10
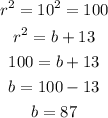
Therefore, the value of b is 87