Question

Can you help me, please?I have to find the coordinates of S, explain why PS=SR, find the coordinates of R, and find the area of triangle PQR.Thank you!

Answer 1

We know that:

`\bar{PQ}\cong\bar{QR}`

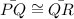
this means that its lengths are equal. We know that the lenght between two points are given by:

`d(A,B)=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Then:

`\begin{gathered} d(P,Q)=\sqrt[]{(4-(-2))^2+(9-0)^2} \\ =\sqrt[]{6^2+9^2} \\ =\sqrt[]{36+81} \\ =\sqrt[]{117} \\ =\sqrt[]{9\cdot13} \\ =3\sqrt[]{13} \end{gathered}`

Now that we have the lenght of side PQ we notice that the point R has to have coordinates of the form (x,0); this comes from the fact that the point is on the x-axis. Using this fact we have that:

`\begin{gathered} d(Q,R)=\sqrt[]{(x-4)^2+(0-9)^2} \\ =\sqrt[]{(x-4)^2+81} \end{gathered}`

Now, using the fact that the sides are congruent we have that:

`\sqrt[]{(x-4)^2+81}=3\sqrt[]{13}`

Solving for x we have:

`\begin{gathered} \sqrt[]{(x-4)^2+81}=3\sqrt[]{13} \\ (x-4)^2+81=117 \\ (x-4)^2=117-81 \\ (x-4)^2=36 \\ x-4=\pm\sqrt[]{36} \\ x=4\pm6 \end{gathered}`

From this we conclude that:

`\begin{gathered} x=10 \\ or \\ x=-2 \end{gathered}`

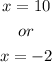
From the figure we notice that the x coordinate of R has to be positive, therefore the coordinate of R is R(10,0).

Now, since the triangle has two congruent sides we conclude that this is an isosceles triangle. We know that the in an isosceles triangle, the altitude having the incongruent side as its base will have the midpoint of that side as its foot, hence we conclude that segments PS and SR are congruent.

Now, from the property stated above we know that S is the midpoint between P ans R. The midpoint is given as:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

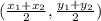
Then point S is:

`\begin{gathered} S((-2+10)/(2),(0+0)/(2)) \\ =S((8)/(2).(0)/(2)) \\ =S(4,0) \end{gathered}`

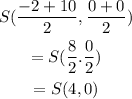
Therefore S(4,0).

Now, we know that the area of a triangle is given as:

`A=(1)/(2)bh`

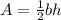
in this case b is the lenght from P to R and h is the lenght from Q to S. with this in mind we have that:

`\begin{gathered} b=d(P,R) \\ =\sqrt[]{(10-(-2))^2+(0-0)^2} \\ =\sqrt[]{12^2} \\ =12 \end{gathered}`

and:

`\begin{gathered} h=d(Q,S) \\ =\sqrt[]{(4-4)^2+(0-9)^2} \\ =\sqrt[]{0^2+(-9)^2} \\ =9 \end{gathered}`

Hence:

`\begin{gathered} A=(1)/(2)\cdot12\cdot9=54 \\ \end{gathered}`

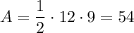
Summing up:

a.

S(4,0)

b.

We know that the in an isosceles triangle, the altitude having the incongruent side as its base will have the midpoint of that side as its foot, hence we conclude that segments PS and SR are congruent.

c.

R(10,0)

d.

A=54 units squared.