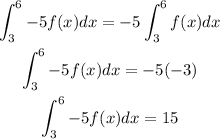Question

Given 3f(x) dx0 = 6 and 6f(x) dx = −33, evaluate the following.

Answer 1

a) 3

b) 3

c) 0

d) 15

Explanations:

Given the following integral functions

`\int_0^3f(x)dx=6\text{ and }\int_3^6f(x)=-3`

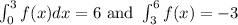
a) We are to evaluate the following integrals:

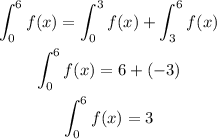
`\begin{gathered} \int_0^6f(x)=\int_0^3f(x)+\int_3^6f(x) \\ \int_0^6f(x)=6+(-3) \\ \int_0^6f(x)=3 \end{gathered}`

b)

`\begin{gathered} \int_6^3f(x)dx=-\int_3^6f(x) \\ \int_6^3f(x)dx=-(-3) \\ \int_6^3f(x)dx=3 \end{gathered}`

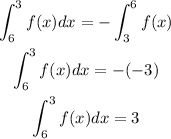
c) For this integral since the upper and lower limit are the same, the integral of the function will always be zero.

`\int_3^3f(x)dx=0`

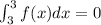
d) Note that every constant inside an integral sign will always come out of the integral. Therefore;

`\begin{gathered} \int_3^6-5f(x)dx=-5\int_3^6f(x)dx \\ \int_3^6-5f(x)dx=-5(-3) \\ \int_3^6-5f(x)dx=15 \end{gathered}`