Question

Find the values of a, b, and c in the equation below.

Answer 1

• a = 12

,

• b = 2

,

• c = 11

Step-by-step explanation

To find the values of a, b, and c, we have to simplify the left side of the equation and try to write that as the product of the variables, like on the right side.

First, apply the distributive property of the exponent over the product,

`((x^5yz^4)^3)/(x^3yz)=((x^5)^3y^3(z^4)^3)/(x^3yz)`

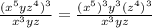
Now, exponents of exponents are multiplied, so we have,

`((x^(5))^(3)y^(3)(z^(4))^(3))/(x^(3)yz)=(x^(5\cdot3)y^3z^(4\cdot3))/(x^3yz)=(x^(15)y^3z^(12))/(x^3yz)`

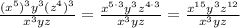
Finally, apply the property of the quotient of exponents with the same base, where the result is the base raised to the difference between the exponents,

`(x^(15)y^(3)z^(12))/(x^(3)yz)=x^(15-3)y^(3-1)z^(12-1)=x^(12)y^2z^(11)`

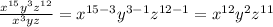
Hence, the values of the unknown exponents are a = 12, b = 2, and c = 11.