Triangles FGE and CDE are similar if their corresponding angles are congruent and their corresponding sides are in proportion Therefore, DE=56.
Triangles FGE and CDE are similar if their corresponding angles are congruent and their corresponding sides are in proportion.
Given that
CE=3x+2, EF=10, DE=5x+1, and EG=16, we can set up a proportion to find DE.
In similar triangles, the ratios of corresponding sides are equal:
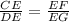
Substituting the given values:
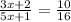
Now, solve for x:
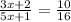
16(3x+2)=10(5x+1)
48x+32=50x+10
32−10=50x−48x
22=2x
x=
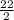
x=11
Now that we have found x=11, let's substitute it back in
DE=5x+1:
DE=5x+1
DE=5(11)+1
DE=55+1
DE=56
Therefore, DE=56.