Question

Let's suppose, in doing a certain statistical study, you take random samples from a population and study the sampling distribution of sample mean. In the next step of the study, you take random samples with a smaller sample size (this means, in the second step, sample size is smaller than previous step) from the same population and study the sampling distribution of sample mean again. Which of the following is true about the parameters of the sampling distribution of the sample mean in both steps?a.In both steps, both the mean and the standard deviation (standard error) remain the sameb.In both steps, the mean remains the same, and in the second step, the standard deviation (standard error) gets smallerc.In both steps, the mean remains the same, and in the second step, the standard deviation (standard error) gets largerd.In second step, both the mean and the standard deviation (standard error) get larger

Answer 1

We have a population of which we take two samples, the first sample size being bigger than the second one.

We have to check each statement about the parameters of the sampling distribution.

We now already that the sampling distribution will have a mean that is equal to the mean of the sample and expected to be non-biased from the population mean. Its value will not depend on the sample size.

On the contrary, the spread of the distribution (standard deviation, for example) will be affected by the sample size: the greater the sample size, the narrower the sampling distribution (in other words, the greater the sample size, the smaller the standard deviation of the sampling distribution).

The parameters of a sampling distribution for samples if size n are:

`\begin{gathered} \mu_s=\bar{x} \\ \sigma_s=(s)/(√(n)) \end{gathered}`

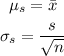
Then, if the second sample has a smaller sample size, its sampling distribution is expected to have a larger standard deviation. The means are expected to be the same.

Then, the correct statement is: in both steps, the mean remains the same, and in the second step, the standard deviation gets larger.

Answer: Option c (In both steps, the mean remains the same, and in the second step, the standard deviation (standard error) gets larger.)