Given: A right triangle ABC
To Determine: The volume of the solid formed if rotated about the segmented BC
Solution
A right circular cone is generated by rotating a right-angled triangle about one of the sides containing the right angle. When we take one side of the right angle as the base and the side perpendicular, as the center and rotate the triangle, it forms a right circular cone.
For the given triangle, we have
So, the new solid is a cone. The volume of a cone is calculated by the formula

Therefore:
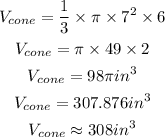
Hence, the volume of the solid to the nearest integer is 308 in³