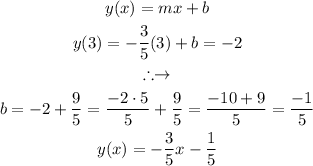Answer:
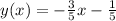
Step-by-step explanation: We need to find the equation of the line in y-intercept form:
Given the two points:

The standard form of the equation of the line is:
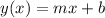
Where:
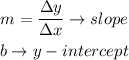
Now, the last step is to find these unknowns from the given information:
Slope:
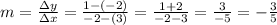
Y-intercept:
We will simply now put one of the points in our standard equation, and extract the y-intercept: