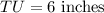Question

In the figure, TU is tangent to the circle at point U. Use the photo to answer the questions. A) Describe the relationship among the lengths of the segments formed by secant, RT, and the tangent segment TU. You may use words/and or an equation.B Suppose RT= 9 inches and ST=4 inches. Is it possible to find the length of TU? If so, who how to find the length or why it is not possible.

Answer 1

Solving part A)

In the figure, we have a tangent line and a secant line. A tangent line is a line that touches the circle only at one point, and a secant line touches the circle at two points.

To find a relationship between the lengths of the segments, we use the secant - tangent rule shown in the following diagram:

In our circle

R is A

S is B

T is C

and

U is D,

Therefore, we can find the relationship using the secant tangent formula:

`RT* ST=(TU)^2`

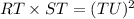
That equation describes the relationship between the lengths of the secant and the tangent.

Solving part B)

For this part, we are given the following values for RT and ST:

`\begin{gathered} RT=9 \\ ST=4 \end{gathered}`

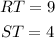
And asked if it is possible to find the length of TU.

The answer is yes, it is possible to find TU by using the equation given in part A.

Substituting the values of RT and ST into the equation:

`\begin{gathered} RT* ST=(TU)^2 \\ \downarrow\downarrow \\ 9*4=(TU)^2 \\ \end{gathered}`

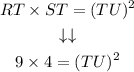
Solving the operations to find TU:

`\begin{gathered} 36=(TU)^2 \\ \sqrt[]{36}=TU \\ 6=TU \end{gathered}`

The length of TU is 6 inches.

Answer:

A)

`RT* ST=(TU)^2`

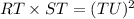
B)

`TU=6\text{ inches}`