Question

What is the molarity? (Question in the photo lol sorry)

Answer 1

The question requires us to calculate the molarity of a Ba(OH)2 solution which pH is 10.20.

To solve this problem, we'll need to go through the following steps:

1) calculate the concentration of H+ ions ([H+]), using the pH of solution provided;

2) calculate the concentration of OH- ions ([OH-]), considering [H+] and the definition of Kw;

3) consider the dissociation of Ba(OH)2 and use [OH-] to calculate the concentration of the solution.

Next, we'll go through these steps:

1) The definition o pH is given as:

`pH=-\log _(10)\lbrack H^+\rbrack`

where [H+] corresponds to the concentration of H+ ions, in mol/L.

We can use this definition to calculate [H+] from pH, as it follows:

`\lbrack H^+\rbrack=10^(-pH)`

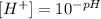
Applying the value of pH provided to the equation above, we'll have:

`\lbrack H^+\rbrack=10^(-10.20)\to\lbrack H^+\rbrack=6.309*10^(-11)mol/L`

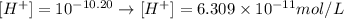
Thus, the concentration of H+ ions in the solution is 6.309 x 10^-11 M.

2) Now, we can use the following definition of the ion-product constant of liquid water:

`K_w=\lbrack H^+\rbrack*\lbrack OH^-\rbrack`

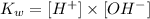
We can rearrange the equation and calculate the concentration of OH- ions, and knowing that Kw value corresponds to 1.01 x 10^-14, we can calculate [OH-]:

`\begin{gathered} \lbrack OH^-\rbrack=(K_w)/(\lbrack H^+\rbrack) \\ \lbrack OH^-\rbrack=(1.01*10^(-14))/((6.31*10^(-11))) \\ \lbrack OH^-\rbrack=1.601*10^(-4)\text{mol}/L \end{gathered}`

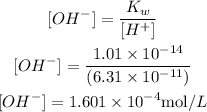
Thus, the concentration of OH- in the solution is 1.601 x 10^-4 mol/L.

3) Next, we need to consider the dissocation of Ba(OH)2 to obtain the concentration of the solution.

Considering that Ba(OH)2 completely dissociates in water:

`Ba(OH)_(2(aq))\to Ba^(2+)_((aq))+2OH^-_((aq))`

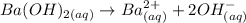
Note that each molecule of Ba(OH)2 would produce 2 ions OH-. In terms of concentration, we can say that the concentration of OH- in solution would be twice the concentration of Ba(OH)2.

Since we calculated the concentration of OH- ions, we can use the relation above to calculate the concentration of Ba(OH)2 by simply dividing [OH-] by 2:

`\text{molarity of Ba(OH)}_2=(\lbrack OH^-\rbrack)/(2)=8.001\text{ }*10^(-5)mol/L`

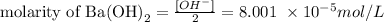
Therefore, the concentration of Ba(OH)2 in solution is 8.001 x 10^-5 mol/L. Note that, since the question required the concentration of solution and not the number of moles, we don't need to consider the volume given for this calculation.

The best option to answer the question would be number 4 (7.92 x 10^-5 M)