Question

How many solutions does this system of equations have? Explain how you know (9x - 3y=-6 5y= 15x+10

Answer 1

hello

we have two equations given and we solve them simultaneously to know how many solutions it has

`\begin{gathered} 9x-3y=-6\ldots eq1 \\ 5y=15x+10\ldots eq2 \\ \end{gathered}`

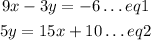
let's rearrange equation 2

`\begin{gathered} 5y=15x+10 \\ 5y-15x=10 \end{gathered}`

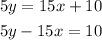
now let's solve from equation 1

`\begin{gathered} 9x-3y=-6 \\ \text{make x the subject} \\ 9x=-6+3y \\ \text{divide both sides by 9} \\ (9x)/(9)=(-6+3y)/(9) \\ x=-(2)/(3)+(1)/(y)\ldots eq3 \end{gathered}`

put equation 3 into equation 2

`\begin{gathered} 5y-15x=10 \\ x=-(2)/(3)+(1)/(y) \\ 5y-15((-6+3y)/(9))=10 \\ 5y+(60-45y)/(9)=10 \\ \text{take the LCM of both sides} \\ (5y+60-45y)/(9)=10 \\ 5y+60-45y=9*10 \\ 60-40y=90 \\ 40y=60-90 \\ 40y=-30 \\ y=-(30)/(40) \\ y=-(3)/(4) \end{gathered}`

put y = - 3/4 into either equation 1 or 2

from equation 2

`\begin{gathered} 5y-15x=10 \\ y=-(3)/(4) \\ 5(-(3)/(4))-15x=10 \\ -(15)/(4)-15x=10 \\ (-15-15x)/(4)=10 \\ -15-15x=10*4 \\ -15-15x=40 \\ -15x=40+15 \\ -15x=55 \\ x=-(55)/(15) \\ x=-(11)/(3) \end{gathered}`

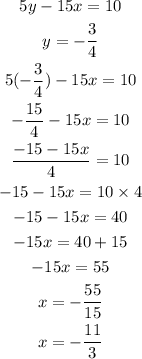
from the calculations above, the system of equations have two solutions.