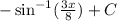Question

Hi! I was shown the problem integral -3/sqrt(64-9x^2)dx but a classmate and was wondering if someone could explain it again. This is the work they showed me

Answer 1

From the problem, we have :

`\int -\frac{3}{\sqrt[]{64-9x^2}}dx`

We need to think of a square number that if we multiply it by 9, the result is 64.

That would be 64/9

`9*(64)/(9)=64`

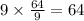
The square root of 64/9 is 8/3.

Let u = 3x/8

8u = 3x

x = 8u/3 (This value is the same as we've got above 8/3)

du = 3/8 dx

dx = 8/3 du

Subsitute x = 8u/3 and dx = 8/3 du

`\begin{gathered} \int -\frac{3}{\sqrt[]{64-9((8u)/(3))^2}}*(8)/(3)du \\ \Rightarrow\int -\frac{8}{\sqrt[]{64-9((64)/(9)u^2)}}du \\ \Rightarrow\int -\frac{8}{\sqrt[]{64-64u^2}}du \end{gathered}`

Extract the square root of 64 which is equal to 8.

`\begin{gathered} \Rightarrow\int -\frac{8}{\sqrt[]{64-64u^2}}du \\ \Rightarrow\int -\frac{8}{8\sqrt[]{1-u^2}}du \\ \Rightarrow\int -\frac{1}{\sqrt[]{1-u^2}}du \end{gathered}`

Note that the identity :

`\int \frac{1}{\sqrt[]{1-u^2}}du=\sin ^(-1)(u)+C`

It follows that :

`\int -\frac{1}{\sqrt[]{1-u^2}}du=-\sin ^(-1)(u)+C`

Bring back u = 3x/8, the answer is :

`-\sin ^(-1)((3x)/(8))+C`