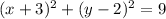Given the center point:
(-3, 2)
Let's find the equation of the circle with the center above which is tangent to the y-axis.
Apply the equation of a circle:

Where (h, k) is the center of the circle and the radius is r.
Since it is tangent to the y-axis, the radius of the circle is the x-coordinate of the center point.
We have:
(h, k) ==> (-3, 2)
r = -3
To write the equation of the circle, we have:

Thus, the equation of the circle is:
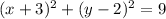
ANSWER: