Question

Drag the tiles to the correct boxes to complete pairs

Answer 1

q(x) = x^2 - 4x + 1

r(x) = 0

b(x) = x - 3

Step-by-step explanation:

Let us do the polynomial long division.

This tells us

`x^3-7x^2+13x-3=\left(x-3\right)\left(x^2-4x+1\right)+0`

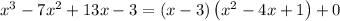
dividing both sides by x - 3 gives

`(x^3-7x^2+13x-3)/(x-3)=(\left(x-3\right)\left(x^2-4x+1\right))/(x-3)+(0)/(x-3)`
`\boxed{(x^3-7x^2+13x-3)/(x-3)=(x^2-4x+1)+(0)/(x-3).}`

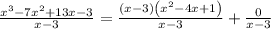
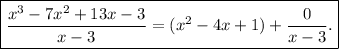
The above tells us that

q(x) = x^2 - 4x + 1

r(x) = 0

b(x) = x - 3.

which are our answers!