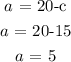Question

mr. ramirez purchased 20 concert tickets for a total of$225. the concert tickets cost $15 for adults and $10 for children under the age of 12part B: solve the system is equations from part A algebraically.show your work

Answer 1

5 adult tickets and 15 children tickets was purchased by Mr. Ramirez

Since we do not know the number of individual ticket types, we represent them with variables

Let the number of adult tickets be a and the number of children tickets sold be c

The sum of both ticket types is 20

Thus, mathematically;

`a\text{ + c = 20}`

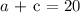
The cost per adult ticket is $15; so the cost of 'a' adult tickets will be 15 * a = $15a

The cost per children ticket is $10; so the cost of 'c' children tickets will be 10 * c = $10c

The sum of both is $225

Thus, we have it that;

`15a\text{ + 10c = 225}`

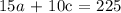
So we have two equations to solve simultaneously

From the first equation, we can have a as the subject of the equation

This will give;

`a\text{ = 20-c}`

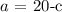
Substitute this in the second equation;

`\begin{gathered} 15(20-c)+10c\text{ = 225} \\ 300-15c\text{ + 10c = 225} \\ 300-5c\text{ = 225} \\ 5c\text{ = 300-225} \\ 5c\text{ = 75} \\ c\text{ = }(75)/(5) \\ c=\text{ 15} \end{gathered}`

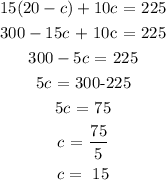
Recall from above;

`\begin{gathered} a\text{ = 20-c} \\ a\text{ = 20-15} \\ a\text{ = 5} \end{gathered}`