Given the value of f(x):
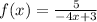
If:

We have that:

To decompose the function, we will look at the function and check if we see any part that might look like a simpler function.
One part that looks like a function is:
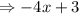
Therefore, let this become our h(x):
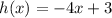
Hence, the composite function becomes:
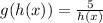
Replacing h(x) with x, we have:
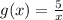
ANSWER:
