The following information is provided in the question:
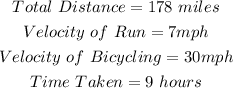
Recall the formula relating distance, speed, and time:
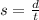
Let the distance for the run be x. This means that the distance for the bicycle race will be 178 - x.
Were we to use the provided information to calculate the time for each part of the race, we would have:
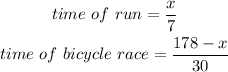
Since the total time is 9, we have:
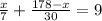
Solving, we have:

Therefore, the distance for the bicycle race will be:
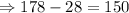
The distance of the run is 28 miles.
The distance of the bicycle race is 150 miles.