Question

I do not understand this problem very well and I would like to know if you could help me. :"/Verify the identity(step)

Answer 1

Given:

tanθ + cotθ = secθ * cscθ

Let's start on the right-hand side, rewriting it by means of these trigonometric identities:

`\begin{gathered} \tan \theta=(\sin\theta)/(\cos\theta) \\ \cot \theta=(\cos\theta)/(\sin\theta) \end{gathered}`

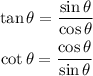
Then, we get:

`\begin{gathered} \tan \theta+\cot \theta=\sec \theta*\csc \theta \\ (\sin\theta)/(\cos\theta)+(\cos\theta)/(\sin\theta)=\sec \theta*\csc \theta \end{gathered}`

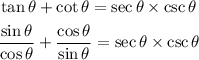
Now, let's divide and multiply the first term on the right-hand side by sinθ, like this:

`\begin{gathered} (\sin\theta)/(\cos\theta)*(\sin\theta)/(\sin\theta)+(\cos\theta)/(\sin\theta)=\sec \theta*\csc \theta \\ (\sin^2\theta)/(\cos\theta*\sin\theta)+(\cos\theta)/(\sin\theta)=\sec \theta*\csc \theta \end{gathered}`

And let's do the same with the second term but with cosθ, like this:

`\begin{gathered} (\sin^2\theta)/(\cos\theta*\sin\theta)+(\cos\theta)/(\sin\theta)*(\cos\theta)/(\cos\theta)=\sec \theta*\csc \theta \\ (\sin^2\theta)/(\cos\theta*\sin\theta)+(\cos^2\theta)/(\cos\theta*\sin\theta)=\sec \theta*\csc \theta \end{gathered}`

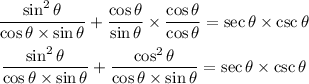
Now that both terms on the right-hand side have the same denominator, let's sum the numerators, like this:

`(\sin^2\theta+\cos^2\theta)/(\cos\theta*\sin\theta)=\sec \theta*\csc \theta`

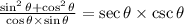
By means of the trigonometric identity:

`\sin ^2\theta+\cos ^2\theta=1`

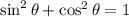
We can rewrite the above expression like this

`(1)/(\cos\theta*\sin\theta)=\sec \theta*\csc \theta`

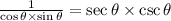
And now, we can separate the denominators, expressing the right side of the equation as a product of fractions, like this:

`\begin{gathered} (1)/(\cos\theta*\sin\theta)=\sec \theta*\csc \theta \\ (1)/(\cos\theta)*(1)/(\sin\theta)=\sec \theta*\csc \theta \end{gathered}`

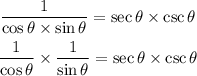
From the trigonometric identities:

`\begin{gathered} \sec \theta=(1)/(\cos \theta) \\ \csc \theta=(1)/(\sin \theta) \end{gathered}`

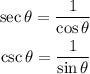
Then, we can rewrite the above expression, like this:

`\sec \theta*\csc \theta=\sec \theta*\csc \theta`

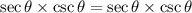
Proved!