Question

Which of the following is the factored form of f(x)f(x) = 2x^2 + 6x - 8A. f(x)= 2(x+4) (x-1)B. f(x) (2x-1) (x+8)c. f(x)= 2(x-4) (x-8)D. f(x)= (2x+1) (x-8)

Answer 1

A. f(x) = 2(x + 4)(x - 1)

Step-by-step explanation

We have the function f(x) given as:

`f(x)=2x^2\text{ + 6x - 8}`

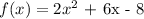
The general form of a quadratic function is:

`f(x)=ax^2\text{ + bx + c}`

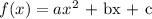
To factor a quadratic equation, we have to find two numbers such that their sum is b and their product is ac i.e. a * c

From the given function, the two numbers we need are 8 and -2.

So, we have:

`\begin{gathered} f(x)\text{ = 2}x^2\text{ + 8x - 2x - 8} \\ Now,\text{ factorise:} \\ f(x)\text{ = 2x(x + 4) - 2(x + 4)} \\ f(x)\text{ = (x + 4) (2x - 2) (collecting like terms)} \\ We\text{ can factor 2 out of the second bracket:} \\ f(x)\text{ = 2(x + 4)(x - 1)} \end{gathered}`

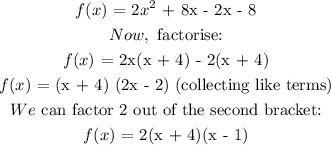
That is the answer.