Given:
Numbers picked from 1 to 30 = 6 numbers
Number of ways = 593775
1 combination = $50,000
Given that the other 593774 combinations result in losing $1, let's find the expected value of losing the game.
Let's first find the number of ways of picking 6 numbers out of 30 numbers.
Apply the combination formula:

The probability of winning will be:
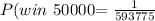
The probability of losing is:
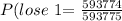
Hence, the expected value will be:

Solving further, we have:
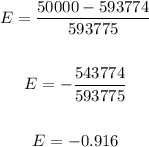
Therefore, the expected value of this game is -0.916
ANSWER:
-0.916