Question

Find the volume of thesolid produced by rotatingthe figure at the rightaround the given axis.

Answer 1

Explanation.

We are given a solid and then told to compute the volume

The solid given is half a hemisphere

The volume of a hemisphere is given by

`Volume=(4)/(3)\pi r^3`

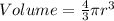
The volume of half the hemisphere will be

`(1)/(2)*(4)/(3)\pi r^3=(2)/(3)\pi r^3`

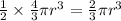
In our case,

`\begin{gathered} r=radius=4m \\ \end{gathered}`

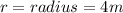
Thus, The volume will be

`\begin{gathered} V=(2)/(3)*\pi* r^3=(2)/(3)*\pi*4^3 \\ \\ V=134.04m^3 \end{gathered}`

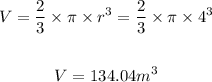
Therefore, the volume of the solid is 134.04m³