Question

Graph the system below and write its solution.**+2-2x+y=-5Note that you can also answer "No solution" or "Infinitely many solutions.

Answer 1

We have the following equation system:

`\begin{cases}y=-(1)/(3)x-1 \\ 2x+y=-6\end{cases}`

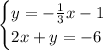
Those are two lines, to plot them you just need two points. The intercepts are the easiest points to calculate. Let's calculate for the first line:

`\begin{gathered} x=0\Rightarrow y=1 \\ y=0\Rightarrow0=-(1)/(3)x-1\Rightarrow x=-3 \end{gathered}`

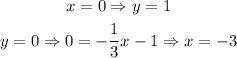
Then, this set of points belong to the first line:

`\lbrace(0,1),(-3,0)\rbrace`

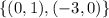
By the same logic, this set of points belong to the second line:

`\lbrace(0,-6),(-3,0)\rbrace`

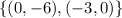
Ploting your system, it should look like this

Coincidentally, we already know the solution because it is on the x-intercept(the point (-3,0)). But let's calculate using our equations.

First, let's rewrite the second equation in slope intercept form.

`2x+y=-6\Leftrightarrow y=-2x-6`

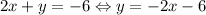
Now we match our equations:

`-(1)/(3)x-1=-2x-6\Rightarrow x=-3`

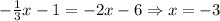
If you evaluate any of the functions at x = -