Given that
There are 75 neighbours.
34 liked daisies
42 liked roses
30 like daffodils
16 liked both daisies and roses
10 liked both daisies and daffodils
20 liked both roses and daffodils 7 liked all three flowers (daisies, roses, and daffodils)
Let 'x' represent the number of neighbours that did not like any of the three flowers.
Let us now represents our data in Venn diagram
The information in the venn diagram represents the following:
1) The number of neighbours that liked daisies only
= 34 - (10-7+7+16-7) = 34 - 19 = 15
2) The number of neighbours that liked roses only
= 42 - (16-7+7+20-7) = 42 - 29 = 13
3) The number of neighbours that liked daffodilis only
= 30 - (10-7+7+20-7) = 30 - 23 = 7
4) The number of neighbours that liked both daisies and roses only = 16 - 7 = 9
5) The number of neighbours that liked both daisies and daffodils only = 10 - 7 = 3
6) The number of neighbours that liked both daffodils and roses only = 20 - 7 = 13
7) The number of neighbours that liked the three flowers = 7
8) The number of neighbours that did not like the three flowers = x
Solving for x
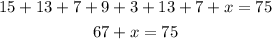
Subtract 67 from both sides
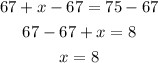
Therefore, the number of neighbours that did not like any of the three flowers is 8.