The question requires us to calculate the molecular mass of a gas, given its density (1.2 g/L) and conditions of pressure (745 torr) and temperature (20°C).
Density is defined as the mass of a compound over its volume. From this definition, we can calculate the molecular mass of the gas knowing the density, as given by the question, and the volume of 1 mol of the gas.
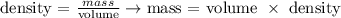
We can calculate the volume of a gas considering the equation of Ideal Gases:

where P is the pressure of the gas, V is its volume, n is the number of moles, R is the constant of gases and T is the temperature.
Note that the constant of gases R was given in units of L.atm/K.mol, while the pressure and temperature were given in Torr and °C, respectively. Thus we need to convert these values to the appropriate units.
Knowing that 1 Torr corresponds to 0.00131579 atm:
1 Torr --------------------- 0.00131579 atm
745 Torr ---------------- x
Solving for x, we have that 745 Torr corresponds to 0.980 atm.
To convert the temperature from Celsius degrees to Kelvin, we must add 273.15:
T = 20 + 273.15 K = 293.15 K
Therefore, the pressure and temperature we'll use in our calculation are 0.980 atm and 293.15 K. Also, since we are calculating the molecular mass, we'll consider 1 mol of gas.
Rearranging the equation of ideal gases to calculate the volume and applying the values to the equation, we'll have:
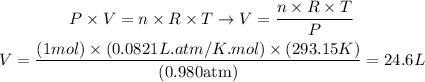
Therefore, the volume of 1 mol of the gas under the conditions given is 24.6L.
Next, we'll use this value to calculate the molecular mass using the density given by the question:
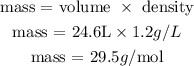
Therefore, the gas given by the question presents 29.5g per mol.