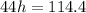Question

Thanh is driving an average of 44 miles per hour, and he is 114.4 miles away from home. After how many hours will he reach his home? Assume Thanh will reach home after h hours. Write an equation to model this scenario. There is no need to solve it

Answer 1

An equation to model this scenario is;

`44h=114.4`

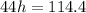
Step-by-step explanation:

Given that Thanh is driving an average of 44 miles per hour, and he is 114.4 miles away from home;

`\begin{gathered} \text{Average speed }v=44\text{mph} \\ \text{distance }d=114.4miles \end{gathered}`

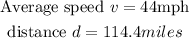
Recall that the distance traveled by an object moving at average speed can be calculated as;

`\text{Average speed }*\text{ time }=\text{ Distance}`

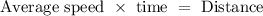
Let h represent the number of hours before Thanh reach home.

Then we have;

`\begin{gathered} v* h=d \\ \text{substituting;} \\ 44* h=114.4 \\ 44h=114.4 \end{gathered}`

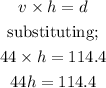
Therefore, an equation to model this scenario is;

`44h=114.4`