Question

Solve each equation with the quadratic formula. Let’s do 43. Here is my work. Having trouble getting the correct answer.

Answer 1

`12x^2-8x-9=0`

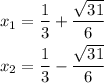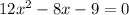
The quadratic formula is:

`x=(-b\pm√(b^2-4ac))/(2a)`

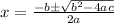
first, we need to identify a, b and c.

a is the coefficient that accompanies the squared term, b is the coefficient to the linear term, and c is the constant term.

`a=12;b=-8;c=-9`

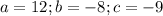
then, we replace the formula with the correct values

`x=(-(-8)\pm√((-8)^2-4(12)(-9)))/(2(12))`

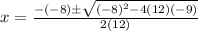
simplify the expression

`\begin{gathered} x=(8\pm√(64+432))/(24) \\ x=(8\pm√(496))/(24) \\ x=(8)/(24)\pm(4√(31))/(24) \end{gathered}`

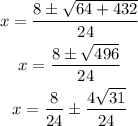
divide into the 2 possible answers and simplify the expression

`\begin{gathered} x_1=(1)/(3)+(√(31))/(6) \\ x_2=(1)/(3)-(√(31))/(6) \end{gathered}`