Question

What are the next 2 term1, 11, 111, 1111 , _, _,

Answer 1

Consider that the given series takes the general form,

`a_n=1^{}+10+10^2+10^3+\cdots+10^n`

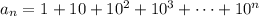
Observe that the expression is in geometric progression with first term 1 and common ratio 10, so applying the formula for the sum of geometric progression, the expression becomes,

`\begin{gathered} a_n=(a(r^n-1))/(r-1) \\ a_n=(1(10^n-1))/(10-1) \\ a_n=(1)/(9)\mleft(10^n-1\mright) \end{gathered}`

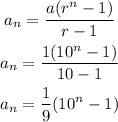
Then the 5th term is given by,

`\begin{gathered} a_5=(1)/(9)\mleft(10^5-1\mright) \\ a_5=(1)/(9)(10000^{}0-1) \\ a_5=(1)/(9)(99999) \\ a_5=11111 \end{gathered}`

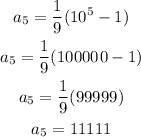
Solve for the 6th term as,

`\begin{gathered} a_6=(1)/(9)\mleft(10^6-1\mright) \\ a_6=(1)/(9)(10000^{}00-1) \\ a_6=(1)/(9)(999999) \\ a_6=111111 \end{gathered}`

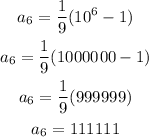
Thus, the next two terms are 11111, and 111111 respectively.