The function that describes the situation is:
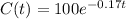
Where C represents the caffeine remaining, and t represents the time.
We want to find t such that C(t)=50. So,
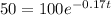
To solve this equation for t, we could use logarithms as follows:

Therefore, it would take 4.08 hours for your body to have only 50mg of caffeine remaining.