For this problem we were given the following system:
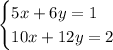
We need to determine how many solutions it has, and if possible find the solutions. The first step is to determine the Matrix that represents this system:
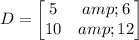
Now we need to calculate the determinant for this Matrix:
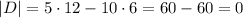
Since the determinant of the system is equal to 0, then it has no solutions. The correct answer is C.