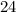Question

CT = x + 3 TE = 2x - 6Find CE.CE=?

Answer 1

The diagonals of a parallelogram intersect at their midpoint. Then:

`CT=TE`

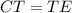
Substitute the expressions for each segment and solve for x:

`\begin{gathered} \Rightarrow x+3=2x-6 \\ \Rightarrow x-2x=-6-3 \\ \Rightarrow-x=-9 \\ \Rightarrow x=9 \end{gathered}`

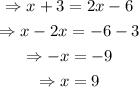
On the other hand, CE=CT+TE. Substitute the expressions for each segment and the value of x to find the length of CE:

`\begin{gathered} CE=CT+TE \\ =x+3+2x-6 \\ =3x-3 \\ =3(9)-3 \\ =27-3 \\ =24 \end{gathered}`

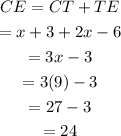
Therefore, the length of the segment CE is:

`24`